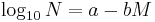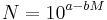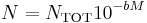Gutenberg–Richter law

In seismology, the Gutenberg–Richter law^[1] (GR law) expresses the relationship between the magnitude and total number of earthquakes in any given region and time period of at least that magnitude.

$\!\,{\log_{10} N} = a - b M$

$\!\,N = 10^{a - b M}$

Where:

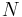$\!\, N$ is the number of events having a magnitude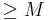 $\!\, \ge M$
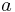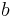$\!\, a$ and $\!\, b$ are constants

The relationship was first proposed by Charles Francis Richter and Beno Gutenberg. The relationship is surprisingly robust and does not vary significantly from region to region or over time.

The constant b is typically equal to 1.0 in seismically active regions. This means that for every magnitude 4.0 event there will be 10 magnitude 3.0 quakes and 100 magnitude 2.0 quakes. There is some variation with b-values in the range 0.5 to 1.5 depending on the tectonic environment of the region.^[2] A notable exception is during earthquake swarms when the b-value can become as high as 2.5 indicating an even larger proportion of small quakes to large ones. A b-value significantly different from 1.0 may suggest a problem with the data set; e.g. it is incomplete or contains errors in calculating magnitude.

There is a tendency for the b-value to decrease for smaller magnitude events. This effect is described as "roll-off" of the b-value, a description due to the plot of the logarithmic version of the GR law becoming flatter at the low magnitude end of the plot. Data which is perfectly following the GR law plots to a straight line. Formerly, this was taken as an indicator of incompleteness of the data set. That is, it was assumed that many low-magnitude earthquakes are missed because fewer stations detect and record them. However, some modern models of earthquake dynamics have roll-off as a natural consequence of the model without the need for the feature to be inserted arbitrarily.^[3]

The a-value is of less scientific interest and simply indicates the total seismicity rate of the region. This is more easily seen when the GR law is expressed in terms of the total number of events:

$N = N_\mathrm {TOT} 10^{-bM} \$

where,

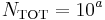$N_\mathrm {TOT} = 10^a \$ , the total number of events.

Modern attempts to understand the law involve theories of self-organized criticality or self similarity.

References

^ Gutenberg and Richter, , pages 17–19 ("Frequency and energy of earthquakes").
^ Bhattacharya et al, p.120
^ Bhattacharya et al, p.119-121
Pelletier, pp.34-36

Bibliography

Pathikrit Bhattacharya, Bikas K Chakrabarti, Kamal, and Debashis Samanta, "Fractal models of earthquake dynamics", Heinz Georg Schuster (ed), Reviews of Nonlinear Dynamics and Complexity, pp.107-150 V.2, Wiley-VCH, 2009 ISBN 3527408509.
B. Gutenberg and C.F. Richter, Seismicity of the Earth and Associated Phenomena, 2nd ed. (Princeton, N.J.: Princeton University Press, 1954).
Jon D. Pelletier, "Spring-block models of seismicity: review and analysis of a structurally heterogeneous model coupled to the viscous asthenosphere" Geocomplexity and the Physics of Earthquakes, American Geophysical Union, 2000 ISBN 0875909787.